Movimiento Circular Uniforme (MCU): Conceptos Fundamentales

El Movimiento Circular Uniforme (MCU) es aquel en el que un objeto describe una trayectoria circular con velocidad angular constante. Es uno de los movimientos más importantes en la física y está presente en muchos dispositivos mecánicos como ruedas, engranajes, motores y en fenómenos naturales como el movimiento de los planetas.

Relaciones entre magnitudes en el MCU

La siguiente tabla resume las relaciones entre las principales magnitudes del MCU:

Características del MCU

• La trayectoria es una circunferencia
• La velocidad angular es constante (ω = constante)
• La velocidad tangencial (lineal) tiene módulo constante pero dirección variable
• Existe aceleración centrípeta, dirigida hacia el centro de la circunferencia

Magnitudes fundamentales del MCU

1. Periodo (T)

Es el tiempo que tarda el móvil en dar una vuelta completa. Se mide en segundos (s) en el SI.

2. Frecuencia (f)

Es el número de vueltas que da el móvil en la unidad de tiempo. Se mide en s⁻¹ o hercios (Hz) en el SI. La relación entre periodo y frecuencia es:

$f=\frac{1}{T}$

3. Velocidad angular (ω)

Es el ángulo recorrido por unidad de tiempo. Se mide en ángulo recorrido, radianes, por segundo (rad/s) en el SI.

$\omega =\frac{\mathrm{\Delta }\theta }{\mathrm{\Delta }t}=\frac{2\pi }{T}=2\pi f$

4. Velocidad tangencial o lineal (v)

Es la velocidad lineal del móvil en cada punto de su trayectoria. Siempre es tangente a la trayectoria circular. Se mide en metros por segundo (m/s) en el SI.

$v=\omega \cdot r=\frac{2\pi r}{T}=2\pi rf$

5. Aceleración centrípeta (a_c)

Es la aceleración que mantiene al móvil en su trayectoria circular. Siempre está dirigida hacia el centro de la circunferencia. Se mide en metros por segundo al cuadrado (m/s²) en el SI.

$a_c=\frac{v^2}{r}={\omega }^{2}r$

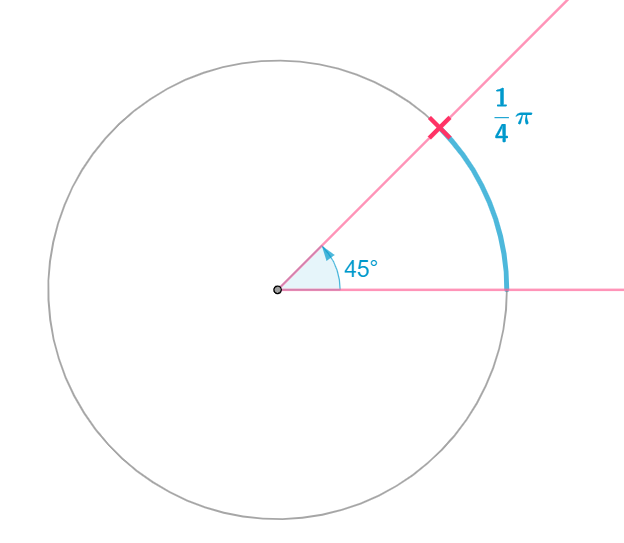
Radianes

El radian es una unidad de medida de ángulos en el Sistema Internacional (SI). Se define como el ángulo subtendido en el centro de un círculo por un arco cuya longitud es igual al radio del círculo.

En términos más simples, un radian es la relación entre la longitud del arco y el radio del círculo:

$\text{Radianes}=\frac{\text{Longitud del arco}}{\text{Radio}}$

Un círculo completo tiene una circunferencia de $2\pi r$, por lo que el ángulo total en radianes es $2\pi$. Esto significa que:

• ${360}^{\circ }=2\pi \text{ radianes}$
• $1\text{ radian}\approx {57.3}^{\circ }$

Los radianes son especialmente útiles en física y matemáticas porque simplifican muchas fórmulas relacionadas con el movimiento circular y las funciones trigonométricas.

Ejemplos resueltos

Ejemplo 1: Un objeto realiza un movimiento circular uniforme con un radio de 2 metros y una velocidad angular de 3 rad/s. Calcular:

a) Su velocidad tangencial:

$v=\omega \cdot r=3\cdot 2=6\text{ m/s}$

b) Su periodo:

$T=\frac{2\pi }{\omega }=\frac{2\pi }{3}\approx 2.09\text{ s}$

c) Su frecuencia:

$f=\frac{1}{T}=\frac{1}{2.09}\approx 0.48\text{ Hz}$

d) Su aceleración centrípeta:

$a_n={\omega }^2\cdot r=3^2\cdot 2=9\cdot 2=18{\text{ m/s}}^2$

Ejemplo 2: Un disco de vinilo gira a 33.33 rpm (revoluciones por minuto). Calcular:

a) Su frecuencia en Hz:

$f=\frac{33.33\text{rpm}}{60\text{s/min}}\approx 0.556\text{ Hz}$

b) Su periodo:

$T=\frac{1}{f}=\frac{1}{0.556}\approx 1.8\text{ s}$

c) Su velocidad angular:

$\omega =2\pi f=2\pi \cdot 0.556\approx 3.49\text{ rad/s}$