Ley de Hooke

La Ley de Hooke es una ley física que describe el comportamiento de los materiales elásticos. Formulada por Robert Hooke en 1660, establece que la fuerza necesaria para estirar o comprimir un resorte es proporcional a la distancia de desplazamiento.

Expresión Matemática

$$ F = -k \cdot x $$

Donde:

$F$ es la fuerza elástica (en newtons, N)
$k$ es la constante elástica del resorte (en N/m)
$x$ es el desplazamiento respecto a la posición de equilibrio (en metros, m)
El signo negativo indica que la fuerza es restauradora, oponiéndose al desplazamiento

Constante Elástica (k)

La constante elástica es una propiedad característica de cada resorte que determina cuánta fuerza se necesita para deformarlo.

Interpretación:

k grande: Resorte muy rígido, difícil de deformar (ej: muelle de un colchón)
k pequeño: Resorte suave, fácil de deformar (ej: goma de borrar)

Unidad: Newton por metro (N/m)

Ejemplo: Resortes con diferentes constantes

Tipo de Resorte	k (N/m)	Características
Resorte muy suave	50	Fácil de estirar
Resorte normal	200	Uso general
Resorte rígido	1000	Muy difícil de deformar

Simulación Interactiva

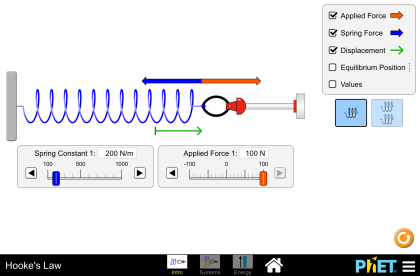
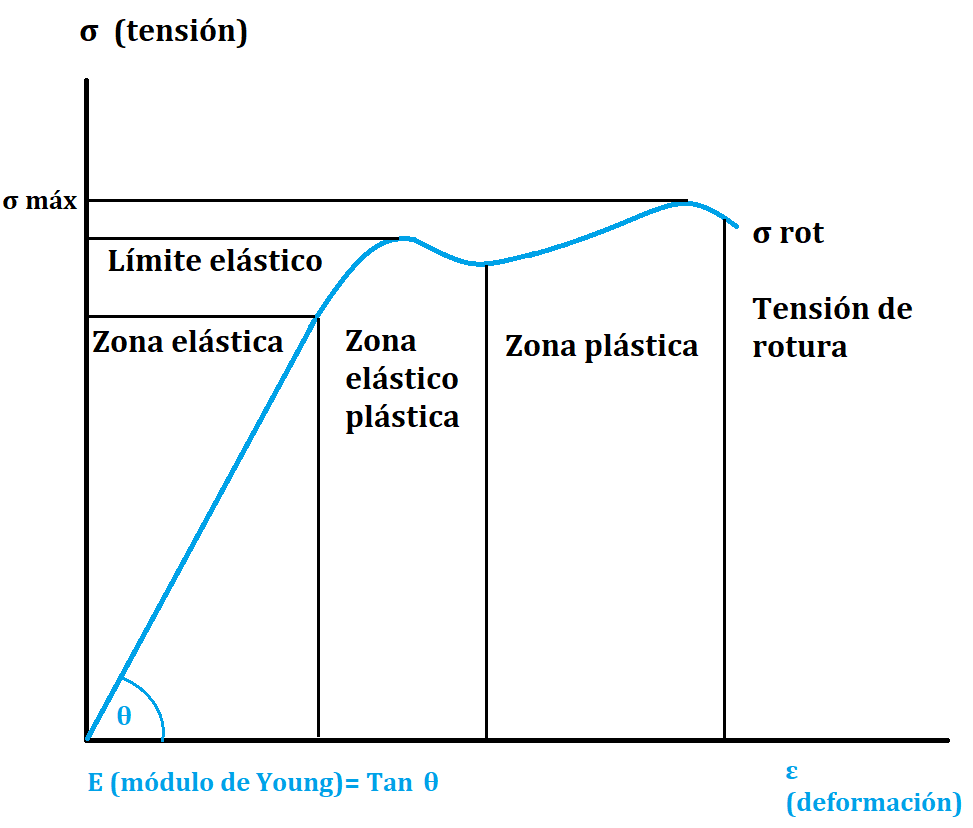
Límite de Elasticidad

La Ley de Hooke solo es válida hasta el límite de elasticidad. Más allá de este límite, el material pierde sus propiedades elásticas.

Regiones de Comportamiento

Región Elástica: Comportamiento lineal

Se cumple la Ley de Hooke
El material recupera su forma original al retirar la fuerza
Deformación reversible

Región Plástica: Comportamiento no lineal

La Ley de Hooke no se cumple
El material sufre deformaciones permanentes
Deformación irreversible

Punto de ruptura: El material se rompe

Energía en Sistemas Elásticos

Energía Potencial Elástica

Cuando se deforma un resorte, se almacena energía potencial elástica:

$$ E_p = \frac{1}{2}k x^2 $$

Esta energía se libera cuando el resorte vuelve a su posición de equilibrio.

Ejemplo: Energía en un resorte comprimido

Un resorte con $k = 200$ N/m se comprime 10 cm = 0.1 m

$$ E_p = \frac{1}{2} \times 200 \times (0.1)^2 = 1 \text{ J} $$

Sistemas Masa-Resorte

Movimiento Armónico Simple

Un sistema masa-resorte es un oscilador armónico simple. Al desplazarse y liberarse, el sistema oscila periódicamente.

Período de Oscilación

$$ T = 2\pi \sqrt{\frac{m}{k}} $$

Donde:

$T$ es el período (tiempo para una oscilación completa, en segundos)
$m$ es la masa (en kilogramos)
$k$ es la constante elástica (en N/m)

Relaciones Importantes

Mayor masa → Oscilación más lenta (mayor periodo)
Mayor rigidez (k mayor) → Oscilación más rápida (menor periodo)
Frecuencia: $f = \frac{1}{T} = \frac{1}{2\pi}\sqrt{\frac{k}{m}}$

Ejemplo: Período de oscilación

Una masa de 0.5 kg cuelga de un resorte con $k = 200$ N/m

$$ T = 2\pi \sqrt{\frac{0.5}{200}} = 2\pi \sqrt{0.0025} \approx 0.314 \text{ s} $$

Frecuencia:

$$ f = \frac{1}{0.314} \approx 3.18 \text{ Hz} $$

Aplicaciones de la Ley de Hooke

Aplicaciones Prácticas

Dinamómetros: Instrumentos para medir fuerzas
Básculas: Utilizan resortes calibrados
Amortiguadores: En vehículos y máquinas
Suspensiones: En sistemas de transporte
Edificios antisísmicos: Utilizan resortes para absorber vibraciones
Instrumentos musicales: Cuerdas de violín, resortes en pianos

Ejemplo: Dinamómetro

Un dinamómetro tiene un resorte con $k = 100$ N/m

Si el resorte se desplaza 5 cm (0.05 m):

$$ F = 100 \times 0.05 = 5 \text{ N} $$

La escala del dinamómetro marcaría 5 N